A problem that pops up from time to time in CUDA is when you want to perform a trivial parallel operation on an input array by assigning one thread per input array element but the number of elements in your input array is larger than the number of threads you have available. Or consider the scenario where you have written some CUDA code which works fine with your GPU however someone else tries to run it with an older model GPU and they run into this problem because their GPU has fewer threads than yours. An elegant way to handle this “more data than threads” problem is to use grid-stride loops within your kernels.
To demonstrate how grid-stride loops work let’s look at a simple CUDA kernel that takes two input arrays of size n and adds them to produce an output array.
__global__
void add(int n, float *x, float *y)
{
int i = blockIdx.x * blockDim.x + threadIdx.x;
if (i < n)
y[i] = x[i] + y[i];
}
As it is now, the kernel does not have a way of handling the case where n is larger than the number of threads that are available. The way that grid-stride loops solves this problem is by wrapping the addition computation in a loop such that each thread performs its addition operation in parallel and then, based on the amount of work that is left to be done, several more parallel iterations of the addition operation are performed (with the same threads) until all the work is done. As the name suggests, the stride of the loop is the total number of threads in the grid (i.e. blockDim.x * gridDim.x).
__global__
void add(int n, float *x, float *y)
{
for (int i = blockIdx.x * blockDim.x + threadIdx.x;
i < n;
i += blockDim.x * gridDim.x)
{
y[i] = x[i] + y[i];
}
}
In the case where n is less than the number of threads available, only one iteration of the loop is performed and the kernel essentially behaves in the same way as the original kernel. In the case where n is larger than the number of threads available, thread i (where i = blockIdx.x * blockDim.x + threadIdx.x) will first perform the addition operation for input i in the first loop iterations. At the end of the first iteration, there will still be n - blockDim.x*gridDim.x data elements that have yet to be computed. So in subsequent iterations, thread i will perform the addition operation for input element i+ blockDim.x*gridDim.x and this process will continue until all input elements have been computed.
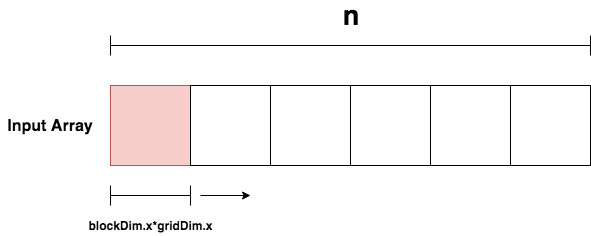
Intuitively, it is like the input is being processed in batches where each batch is processed in parallel. Therefore using grid-stride loops, a kernel can handle input sizes that are much larger than the threads you have available.
Thank you for reading.