A CUDA Implementation of the K-Means Clustering Algorithm
This blog post will cover a CUDA C implementation of the K-means clustering algorithm. K-means clustering is a hard clustering algorithm which means that each datapoint is assigned to one cluster (rather than multiple clusters with different probabilities). The algorithm starts with random cluster assignments and iterates between two steps
- Assigning datapoints to clusters based on the closest centroid (by some distance metric).
- Updating the centroids based on the new cluster assignments from the previous step.
Eventually the cluster assignments converge giving the final result. In this CUDA implementation each of the two steps will be performed in parallel. The implementation is for the 1-dimensional case where each datapoint is a scalar but it could easily be extended to the multi-dimensional case.
Assigning Datapoints to Clusters
The first step is assigning datapoints to their nearest centroid . This step is not difficult to parallelize because the distance computations can be performed independently for each datapoint.
__global__ void kMeansClusterAssignment(float *d_datapoints, int *d_clust_assn, float *d_centroids)
{
//get idx for this datapoint
const int idx = blockIdx.x*blockDim.x + threadIdx.x;
//bounds check
if (idx >= N) return;
//find the closest centroid to this datapoint
float min_dist = INFINITY;
int closest_centroid = 0;
for(int c = 0; c<K;++c)
{
float dist = distance(d_datapoints[idx],d_centroids[c]);
if(dist < min_dist)
{
min_dist = dist;
closest_centroid=c;
}
}
//assign closest cluster id for this datapoint/thread
d_clust_assn[idx]=closest_centroid;
}
The above code is actually very similar to the serial case. Here the thread index idx corresponds to the index of the datapoint. The rest of the code is pretty straight-forward. This distance between the datapoint d_datapoints[idx] and each centroid d_centroids[c] is computed and the centroid that is closest is then assigned to that datapoint. One drawback of this code is that the centroids and datapoints are read from global memory which is somewhat slow.
The distance function used here is simply the Euclidean distance for the 1-d case.
__device__ float distance(float x1, float x2)
{
return sqrt((x2-x1)*(x2-x1));
}
Updating Centroids
The next step is to recompute the centroids given the cluster assignments computed in the previous step. This is much more tricky to parallelize since the centroid computations depend on all of the other datapoints in its cluster. However, operations that rely on distributed datasets to compute a single output value can still be parallelized and are called reductions. A sum reduction is shown in the diagram below.
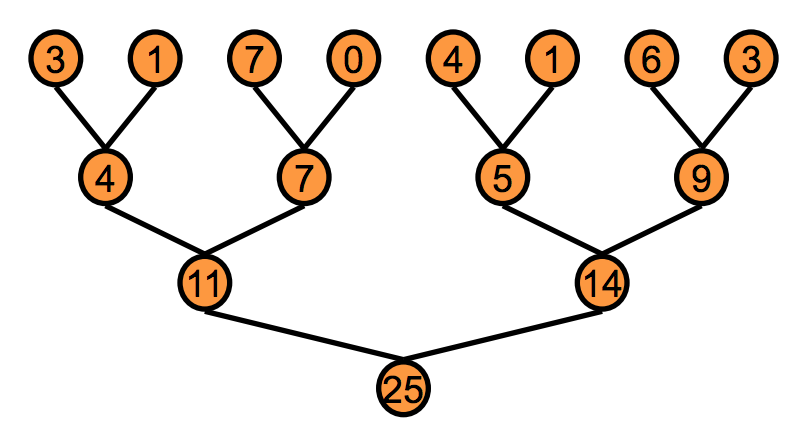
The general procedure is to partition the input array and perform the sum on each partition in parallel then merge the partitions and repeat the process until all partitions have been merged and you are left with the final sum value. This parallelization allows for logarithmic complexity rather than linear as with the serial case.
The centroid recomputation can also be thought of as a reduction operation and the code is shown below.
__global__ void kMeansCentroidUpdate(float *d_datapoints, int *d_clust_assn, float *d_centroids, int *d_clust_sizes)
{
//get idx of thread at grid level
const int idx = blockIdx.x*blockDim.x + threadIdx.x;
//bounds check
if (idx >= N) return;
//get idx of thread at the block level
const int s_idx = threadIdx.x;
//put the datapoints and corresponding cluster assignments in shared memory so that they can be summed by thread 0 later
__shared__ float s_datapoints[TPB];
s_datapoints[s_idx]= d_datapoints[idx];
__shared__ int s_clust_assn[TPB];
s_clust_assn[s_idx] = d_clust_assn[idx];
__syncthreads();
//it is the thread with idx 0 (in each block) that sums up all the values within the shared array for the block it is in
if(s_idx==0)
{
float b_clust_datapoint_sums[K]={0};
int b_clust_sizes[K]={0};
for(int j=0; j< blockDim.x; ++j)
{
int clust_id = s_clust_assn[j];
b_clust_datapoint_sums[clust_id]+=s_datapoints[j];
b_clust_sizes[clust_id]+=1;
}
//Now we add the sums to the global centroids and add the counts to the global counts.
for(int z=0; z < K; ++z)
{
atomicAdd(&d_centroids[z],b_clust_datapoint_sums[z]);
atomicAdd(&d_clust_sizes[z],b_clust_sizes[z]);
}
}
__syncthreads();
//currently centroids are just sums, so divide by size to get actual centroids
if(idx < K){
d_centroids[idx] = d_centroids[idx]/d_clust_sizes[idx];
}
}
In the above code, s_idx refers to the thread at the block-level (i.e. multiple threads will have the same s_idx assuming more than one block is being used). The next bit of code
__shared__ float s_datapoints[TPB];
s_datapoints[s_idx]= d_datapoints[idx];
__shared__ int s_clust_assn[TPB];
s_clust_assn[s_idx] = d_clust_assn[idx];
is the partition step of the reduction where the global datapoint (d_datapoints) and cluster assignment (d_clust_assn) variables are brought into shared memory for the block that thread idx is in.
The next bit of code is only executed within the first thread of each block (i.e. if(s_idx==0)...). This thread creates two variables local to that thread - b_clust_datapoint_sums which is an array of length K that holds the sums of the datapoints assigned to each cluster and b_clust_sizes which is also an array of length K that holds the sizes of each cluster. The thread then traverses the datapoints and cluster assignments in the shared memory for its block and accumulates the results in these local variables.
The next step is to combine these intermediate results into the global variables d_centroids and d_clust_sizes to get the final update result. This is done with the atomicAdd function which ensures that race conditions will not occur when multiple threads are writting to the same place. However, we don’t want our centroids to be sums so the last step is to divide the sums by the cluster sizes which can be done in parallel at the global thread level.
Thanks for reading and checkout the full code on github.